Golden Age Cremonese Mean (GACM) Arching Profiles
Many makers of archtop instruments desire a simple formula that can be used to describe the arching profiles used in classic violins. This turns out to be impossible, the major obstacle being that the contours of classic violins are all quite different from each other. Recent published research has generated arching profiles made by averaging profiles from a number of golden age Cremonese violins, and has provided a formula for rendering these profiles. Included here is a calculator that can be used to calculate these profiles such that they can be imported into drawing or spreadsheet software.
Initial appearance: July 20, 2012
Last updated:
June 19, 2025
Contents
Transverse Arching Profiles of Violins
A lot of modern violin makers render the arching contours of the plates in the same manner that they have probably been rendered since the appearance of arched plate instruments, by eye and by successive approximation. The plate blank is assembled and then thicknessed to near the ultimate height of the arch. The neck end, tail end and sides are then planed down in a tapered fashion so that the blank looks like a squat and flat topped pyramid. The outline of the plate is then cut out and the thickness of the edges marked on the sides. The space between the top and edges of the blank is then progressively carved down until it resembles the familiar shape.
This ad hoc method works out well and some of the very best instruments are made in this manner. Some folks produce close copies of famous instruments and for these the contours of those famous instruments are closely matched, making use of templates created from measurements of those instruments.
From time to time someone will opine that the graceful curves of violin plate arching follows some mathematical form. But although it is certainly possible to represent the curve of any arching profile with a polynomial function, there really is no way to represent all curves on all instruments with such a function. Why this is so will be obvious from the following figure.
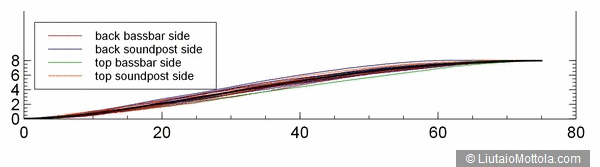
What we are looking at here are all of the upper bout arching profiles from the nadir (lowest point) of the recurve to the apex of the curve at the instrument centerline, taken from five famous golden age Cremonese instruments selected at random. There are 20 profiles in the graph. The curves have all been normalized to the same length and height and some have been mirrored so that curves from both sides of the instrument and from both plates can be compared. As is obvious from this figure, although all of these profiles share the same basic characteristics, they are all very different from each other. Although it is not apparent at the magnification of this figure, the curves differ dramatically not only from instrument to instrument but also among curves at this position for the same instrument. Again, a single simple formula that represents this entire range of shapes is just not possible.
Golden Age Cremonese Mean (GACM) Arching Profiles
But there is some demand for arching curves that can be described in simple mathematical terms. Instrument builders that start their design with CAD drawings or that want to carve (or rough carve) plates using CNC machinery could use such arching profiles. And then there are hand builders that simply want to start with simple symmetrical curves for all their instruments.
The most recent attempt that I know of to describe violin arching curves in simple mathematical terms makes use of curtate cycloid curves1. Unfortunately these turn out not to represent golden age violin arching profiles very well2 and certainly can't represent the wide variety of curves indicated in the figure above. As mentioned, it is possible to calculate a polynomial for each profile curve of a particular instrument, and this is one approach to the problem. Another approach would be to take the average of profile curves at each position from a number of famous instruments and then to describe these average curves mathematically. This way, although you don't get a set of curves which match any one classic instrument, you do get a set of curves which contains the essence of all of them. Maybe. Recent research3 describes just such a process. If you take a look at the above figure again you'll notice a thicker black line among the various colored lines. This is the mean upper bout arching profile of five golden age violins. The research referenced generated these mean curves (called ensemble averages) for upper bout, C bout and lower bout from the five Cremonese instruments. I refer to these here as Golden Age Cremonese Mean (GACM) transverse arching profiles. It turns out that a fairly simple formula can be used to specify points on any of these curves. If you can specify the length and height of the curve, that formula can be used to draw the curve.
Javascript Calculator
The actual formula is included in the original research paper. It is a bit hairy to use, but here is a calculator that will do the math for you. The calculator generates a list of points for a half transverse GACM arching profile with either a fixed x interval or a fixed y interval. The calculator takes the following arguments:
Length of half profile
The length of the half transverse GACM arching profile;Total height
The total height of the profile;X offset (indent)
The script assumes that you are using the output to generate curves for the contour of a plate. This value indicates how far in from the edge of the plate the curve should start. It is added to each x coordinate value generated by the script;Y offset (thickness)
This value is equivalent to the thickness of the plate at the start of the arch. It is added to each y coordinate value generated by the script. This value must be less than the total height;Number of points
The number of data points you want generated;Here is how these parameters relate to a typical transverse arching profile:

Note that the x or y interval is specified implicitly. When requested to generate a list of points for a half profile with a fixed x interval, the calculator uses (the length - the x offset) divided by (the number of points - 1) as the x interval. When requested to generate a list of points for a half profile with a fixed y interval, the calculator uses (the total height - the Y offset) divided by (the number of points - 1) as the y interval.
Note also that the ratio Length:(Height - Y offset) cannot exceed 4:1. If you try to make a curve that's higher than that the results get real strange.
You can specify the format you want for the output. The calculator will generate a tab delineated .csv file for use by a spreadsheet, a .dxf file containing a polyline representing the specified curve in default units for use by CAD drawing software, or an .svg file containing a polyline representing the specified curve in default units for use by artistic drawing software. The calculator can also generate a coordinate list output in a popup window. If you specify this option be sure to allow popups for this website. The coordinate list is output as a list suitable for copying to the clipboard and then being pasted into a spreadsheet or other program for further use.
Here's the calculator which generates a list of points for a half transverse GACM arching profile:
Calculating Points on a Transverse GACM Arching Profile Curve
The calculator uses a successive approximation algorithm when calculating curves with fixed y interval, and as Javascript is an interpreted language, execution can take a little while for long lists of points. A status field shows the progress. Note that the calculator yields values with four decimal places of precision. This is generally more than adequate for units of inches or centimeters, for plotting curves or machining plates. If you use the calculator to generate a huge number of points though, there is the possibility of generating duplicate points. If you notice duplicate points in the data output the best bet is to simply decrease the number of points you are generating.
References and Suggestions for Further Reading
Playfair, Q. “Curtate Cycloid Arching in Golden Age Cremonese Violin Family Instruments” CAS Journal, Vol. 4 ( No. 7 (Series II)), pp. 48-58.
Mottola, R.M. “Comparison of Arching Profiles of Golden Age Cremonese Violins and Some Mathematically Generated Curves” Savart Journal, Vol. 1 ( No. 1)
Mottola, R.M. “Visual Comparison of Ensemble Averaged Transverse Arching Profiles of Golden Age Cremonese Violins and Curtate Cycloid Curves” Savart Journal, Vol. 1 ( No. 2)


